Direct and indirect measurement
An important idea for the concept of measuring is the practical fact that in the environment, things can be touched or accessed for measurement either directly, or indirectly. We measure things directly, by physically accessing them and comparing their size to that of recognized standard size units. We measure indirectly by using alternative access means, and then performing convenient transformations, manipulations, calculations, analysis and/or derivations. Common examples of quantities that are indirect (compounded or calculated ) by nature are : speed, pressure, density, economic worth, etc.

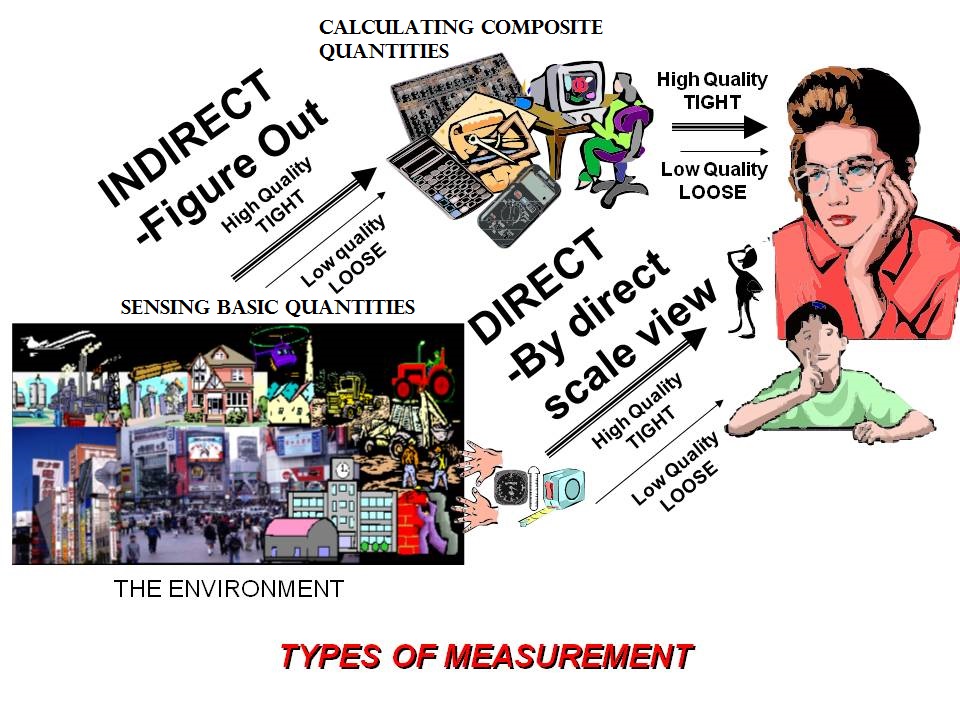
Measurement can therefore be executed directly or indirectly, depending on the physical availability or accessibility of the things being measured, or the applicable instruments and procedures. In summary:

• Direct measurement occurs when instruments can have direct physical access to, placed in direct contact with or in view of the objects being measured, providing opportunity for readily available comparison to reference units, groups of units, or counts in a graduated (tickmarked) scale. The quality of direct measurements will clearly depend on the accuracy and precision supported by the instruments and procedures used.

• Indirect measurement occurs when instruments cannot, or are not available or chosen to provide direct reference scale value readings for the objects being measured. Assessments are therefore determined indirectly, by measuring related, more convenient quantities instead, and then deriving or calculating the quantities of interest from these.

The quality of indirect measurements will therefore depend not only on the accuracy and precision afforded by the direct measurement of the base supporting quantities, but also on the accuracy and reliability of the procedures and instruments used to derive or calculate the desired values. A view of the options (and quality) choices for direct and indirect, gross (loose) and fine (tight) measurement is shown in the figure below.

Call the Measuring weight display to observe and play with a simple example of direct and indirect measurement.  

HANDS ON:  Interactive screen/wired/wireless-mouse or touch-sensitive

1.- Turn the digital scale POWER on (center-top) , place a red cube on the platform of the scale, and read the quantity displayed on its (digital) numeric screen. This is an example of direct measurement of the weight of the cube. Write down the measured weight of the cube.

2.- Move the red cube from the platform of the scale to the left side tray of the balance underneath.

3.- Place the pencil on the right side tray of the (tilted) balance.

4.- Repeatedly add one-gram standard weights to the left side tray of the balance, until equilibrium (untilted, equal weight, or "balance") is reached.

5.- Use the information gathered in steps 1 and 4 to figure out indirectly the weight of the pencil.

What is the weight of the pencil? 7 grams

Now find the exact weight of each of the items at the right side of the scale using any direct or indirect method you choose.

Blue cube: 4 grams

Red cube: 4 grams

Pencil: 7 grams

Nut: 11 grams

Dog: 82 grams

Apple: 122 grams

Wood cube: 174 grams

Tractor: 227 grams

ALGEBRA AS A TOOL FOR INDIRECT MEASUREMENT

Call again, or press the RESET button of the Measuring weight display, and now focus attention on the balance section at the bottom. There we find: an empty balance, small Grade "Level" buttons (K, 1, 2+), a button labeled "Problem #", a small text window, a "No. Correct" counter, and a data entry section with keys, numeric display, and an "Enter" button. The Grade Level buttons restrict the objects available for weighting by magnitude, the text window will present a new "algebra problem" -equation every time it is pushed, the data entry section allows for the entry and view of the numerical "solution" proposed as a correct answer to the problem presented.

The small numeric window next to the Enter button will record the proposed number-answer, while the small lower (yellow) display below will show proposed solutions and verification results. After verification, the display will either sound out and display an incorrect answer, or display the proposed number with a checkmark and sound acknowledging a correct response. Each answer to a new problem presented would be determined only by observing the shown conditions and compared with the implied relationship described by the equation in view, as well as results obtained previously in the sequence.

• Please call each of the 20 different problems proposed by the display, and make sure to exercise either mentally, or a written form the calculations necessary (without using any form of direct measurement) to indirectly determine (measure) the weight of the items requested by the equation related to each problem. After finding each correct solution, implement the physical actions implied by the equation and observe the solution.

INDIRECT MEASUREMENT AND GEOMETRY

Geometry, sometimes called the “mathematics of form”, deals with the identification, measurement, manipulation, combination and prediction of size, position, coordination and effects of quantities thought of as shapes and patterns. Measuring in geometry uses both direct and indirect measurement - through the use of analysis and formulas. The following are some of the most important terms in basic Geometry:

Length, height and width : The straight distance across the extreme points of an object in horizontal, vertical in depth-wise directions. Examples of use: How high, wide, or deep is a water container, or a combination of containers of different shapes and/or sizes?

Call the Making Volume and the Repeated Accumulation of Effects and Exponents displays to observe the creation of regular sided shapes or visualizations with (perpendicular/orthogonal/right-angled) growth in three different directions (dimensions).

Perimeter:  The length of the edges of a closed surface, or the continuous line that surrounds a surface. Examples of use: how long is the wood strip around a picture frame, or how long is the fence around a field, or a border to a country...

Area: The size of a contiguous cover, skin, or surface. Examples of use: How much carpet, tiles or square surfaces we need to cover a room floor, a water surface or extent of farming or parkland?

Surface Area (of a container): The total extent of an area, areas, or skin covering all sides of a three-dimensional body or a container. Examples of use: How much gift wrapping paper we need to cover all the sides of a gift box, or paint to cover a building? How much area of land is needed for growing a crop?

Volume (capacity of a container): The containing capacity inside an object.  How much water, milk, or air can a container bottle hold inside?

In geometry, there are eight basic, “regular” (i.e. nicely shaped) forms or shapes of interest:

BASIC GEOMETRIC SHAPES

These basic shapes are important, because much of our ability to understand and build things in real life is based on the knowledge of these basic shapes.

Call the Measure Basic Shapes display.

This display features the direct measurement of the first two dimensional features (perimeter and area) of the four basic shapes (square, rectangle, triangle, circle), using direct procedures (a ruler and overlay grids), scaled (marked) in either metric units (centimeters, square-centimeters) or English units (inches, square-inches).  The activity presents and relates a direct measurement tool (ruler), with formulas and calculations that are common in school curriculum. A detailed explanation of the calculation process for these shapes and for capacity /volume is the topic of the next section ahead.

HANDS ON:  Interactive screen/wired/wireless-mouse or touch-sensitive

1.- Select each group of shapes by clicking/touching each of the shape-selection bars at the top of the display (Squares, Rectangles, Triangles, Circles, and the Little person).  The groups of shapes will be displayed correspondingly.  Click and drag the transparent ruler, the square-centimeter-sheet, and the square-inch-sheet to explore their use in measuring shapes.  Use the (green) buttons on the transparent ruler to rotate it as needed. 

Click on the keys in the entry-pad to observe the creation (and reset) of numbers, and experience calculation of squares and multiplying by Pi as needed. Clear/reset an entry by clicking on the numeric display itself.

The numbers displayed in the entry-pad can be entered by pointing and clicking into corresponding “Perimeter” or “Area” cells in the column boxes under the selection bars.

The SQUARE shape

2.- Click on the Squares shape-selection bar.  One at a time, the transparent ruler, the centimeter-overlay, or the inches-overlay could be placed over each square shape, to measure (as close as possible approximately) the length of the surrounding edges (PERIMETER) and the extent (size) of the AREA inside Each AREA and PERIMETER number found should be "clicked in" to enter it into the corresponding box of the shape rows. NOTE: When the numbers are correct (within one-half of a unit), the entry box in the array will signal it by clearing (white) the box area and offering an arcade-beep sound. When the number is incorrect, the box area will turn gray, and an error "coo-coo" sound will be heard. MAKE SURE to have the correct "Metric (centimeters)" or "English (inches" option box checked in before entering the numbers. NOTE: Changing the option of units of measure will clear (reset) all the numbers currently entered in each and all number boxes.

"The following paper-and-pencil basic shape model form can be used to record the corresponding measurement for and perimeter and area numbers all of the different size shapes shown, and in both, metric (centimeters) and English (inches) units.

The TRIANGLE, RECTANGLE, and CIRCLE shapes

3.- One at a time, call each of the remaining three basic shapes (Rectangle, Triangle, Circle), and make sure to complete all the boxes for each shape, as well as those for the additional "Little person" profile included in this activity (a total of 8 boxes each shape), before moving to the next section.

4.- Make sure to complete all boxes each for the centimeters and inches options allowed.

QUESTION: Why are the numbers in Centimeters and Inches for perimeter and area are different numbers, if we are measuring the same things? ______________________________________________
                                      ( because each inch represents a length of 2.54 centimeters ) 

QUESTION: How do we deal with the measurement and calculation when working with nature's curved shapes (e.g. a plant, animal, field or lake)?

______________________________________________
                                      ( By using and counting -integrating- smaller bits of line or square units to measure tighter spaces. In the extreme and for accuracy, we could consider what are called "differential size" squares and grids , including graphic “pixels”, or calculating in what we call "differential and integral calculus". )

MEASURING VOLUME /CAPACITY AND SURFACE AND DEVELOPING "FORMULAS" FOR BASIC SHAPES

Call the BASIC GEOMETRY display.

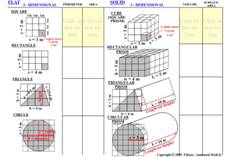
In the display, we can observe, use our common sense and obtain measurements for perimeter, area, surface areas, and volumes of the simplest shapes in basic geometry. The units of length for edges are the standard metric system units called meters (m).  The units of area for surfaces are square-meters (m2 - a unit square with one-meter each side ), and the units of content for volume are cubic-meters (m3 - a unit cube with one unit square side each side wall).  

Although the metric system is used in most everywhere else in the world, in the United States, the prevailing units of measurement are those of the English System.  As a consequence, we have inches, feet, yards, miles, for length, and square and cubic units of these for area and volume, as well as others such as fluid-ounces, etc.

HANDS ON:  Interactive screen/wired/wireless-mouse or touch-sensitive

1.- Identify, one by one, the four “FLAT 2-dimenssional” and “SOLID 3-dimensional” shapes included in the display, and notice the “Perimeter”, “Area”, “Volume”, and “Surface area” columns.

The SQUARE and the CUBE

Focus on the square shape, its edges, and the unit of measurement for the perimeter (red, “1 linear meter”).

 2.- Click once over the (yellow) box next to the square, at the top of the PERIMETER column. This will to begin an animation of the measurement of the perimeter of the square.  Click on a few more times, until all 12 meters of the perimeter are highlighted in red.  

Do the perimeter animation again one step at a time, and focus on the text appearing on the activating (yellow) box. The gradual construction of the formula (quick, automatic procedure) for the perimeter of the square is shown inside the activating box.

Focus on the flat surface inside the square, and the small, flat-square (gray, “1 square meter”) of unit measurement for the area.

 3.- Click once over the second yellow box to the right of the square, in the AREA column. This will to begin an animation of the measurement of the area of the square.  Click on a few more times, until all 9 square meters that make up the total shape and area are highlighted gray.  

Do the area animation again one step at a time, and focus on the text appearing on the activating box. The gradual construction of the formula for the area of the square is shown.

Focus on the “SOLID 3-dimensional” column, and the CUBE (SQUARE PRISM) shape at the top. The surface of a cube is a construction made with several squares, identical to the one observed in the previous activity.  Figure out: how many squares make up the whole surface of the cube?.
The cube also has an interior, and that it can be used to contain material. That the size of the interior, called volume can also be measured, by using unit cubes (gray, “1 cubic meter”) of content.

The cube is also a construction made with accumulating “slices” of squares with unit cubes on top of them. How many slices  make up the cube?

4.- Click once over the (yellow) box next to the right of the cube, at the top of the VOLUME column. This will to begin an animation of the measurement of the volume of the cube.  Click on a few more times, until all 27 cubic meters of the volume are highlighted gray.  

Do the volume animation again one step at a time, and focus on the text appearing on the activating box. Observe the gradual construction of the formula for the volume of the cube.

Focus on the flat surfaces covering the cube, and the fact that the total area of the cube’s surface is the sum of the areas covering it.  Ask them to figure out: how many large flat surfaces make up the surface of the cube?.

4.- Click once over the (yellow) box second to the right of the cube, at the top of the SURFACE AREA column. This will to begin an animation of the measurement of the surface area of the cube.  Ask the same student to click on a few more times, until all 54 square meters of the surface area are highlighted gray.  Make sure that the students acknowledge the “Double (x2) for three equal sides behind” note.

Ask another student to do the surface area animation again one step at a time, and focus on the text appearing on the activating box. Explain the gradual construction of the formula for the surface area of the cube.

OTHER BASIC SHAPES

RECTANGLE and RECTANGULAR PRISM

Focus on the rectangle shape.

 2.- How long do you think the line corresponding to the PERIMETER of the rectangle will be?   _______ ( 14 meters )

 3.- What could be a formula for a quick calculation of the perimeter of the rectangle?
____________________ ( p = 2w + 2h meters )

Now focus on the (flat) surface inside the rectangle, and the small, flat gray-square unit of measurement for the area.

4.- What would be the area  of the rectangle (total number of unit rectangles)? ________  ( 12 square meters, or m2 ) 

5.- What would the formula for a quick calculation of the area of the rectangle?  
______________________ ( a = w x h  square meters, or m2 )

Now focus on the SOLID 3-dimensional RECTANGULAR PRISM shape.

6.- What would be the volume (or internal content capacity) of the rectangular prism?     HINT – ALTHOUGH THE UNIT CUBES CAN BE COUNTED INDIVIDUALLY, IT MIGHT BE MORE EFFICIENT IF THINKING OF THE PRISM AS A STACK OF EQUAL VOLUME SLICES, THEN COUNTING, OR CALCULATING THE VOLUME OF A SINGLE SLICE, AND THEN ADDING (OR MULTIPLYING FOR SPEED) TO GET THE TOTAL FOR ALL OF THE SLICES IN THE PRISM: ________  ( 60 cubic meters, or m3 ) 

7.- What could be a formula for a quick calculation of the volume of the rectangular prism?   ________________________ ( v = w x h x L cubic meters, or m3 )

5.- What could be a formula for a quick calculation of the surface area of the rectangular prism?  
_______________________________ ( Sa = 2(w x h) + 2(w x L) + 2(h x L) square meters, or m2 )

TRIANGLE and RECTANGULAR PRISM

Focus on the (flat) triangle shape.

 2.-How long do you think the PERIMETER of the triangle will be?   _______ ( 4.2 + 4 + 3.1 = 11.3 meters )

 3.- What could be a formula for a quick calculation of the perimeter of the rectangle?
____________________ ( p = 2w + 2h meters )

4.- What would be the area  of the rectangle (total number of flat unit squares contained inside)?     HINT – THE UNIT SQUARES AND PARTS OF UNITS CAN BE COUNTED INDIVIDUALLY, AND COMBINED.  FURTHERMORE, WE COULD ENVISON A LINE THAT GOES STRAIGHT UP FROM THE BOTTOM OF THE TRIANGLE, TO THE TIP (VERTEX) ON THE TOP END, CALLED THE “height”.  SUGGEST THAT ON BOTH SIDES OF THE height LINE, THERE ARE TWO “HALF RECTANGLES”, BELONGING TO THE TRIANGLE.                       ________  ( 6 square meters, or m2 ,  or the combined area of two half-rectangles:  (3 x 3)/2, plus (3 x 1)/2  =  4.5 + 1.5  ) 

5.- Ask the students:  What could be a formula for a quick calculation of the area of the triangle?  
______________________ ( a = (b x h)/2   square meters, or m2 )

Now focus on the SOLID 3-dimensional TRIANGULAR PRISM shape.

6.- What would be the volume of the triangular prism? ________  ( 60 ) 

7.-  What could be a formula for a quick calculation of the volume of the rectangular prism?    HINT – EVEN THOUGH THE VOLUME OF ANY PRISM CAN BE FOUND BY COUNTING ALL THE UNIT VOLUME PIECES AND PARTS INDIVIDUALLY, a more efficient way would be BY FIGURING UP THE VOLUME OF ONE SLICE, AND THEN ADDING UP (multiplying) by ALL THE equal slices THAT MAKE UP THE LENGTH OF THE PRISM.

 ______ ( v = ( ( b x h )/2) x L, OR  ( b x h x L )/2  cubic meters, or m3 )

8.- What could be a formula for a quick calculation of the surface area of the triangular prism?    HINT – MENTION THAT THE SURFACE AREA IS MADE UP BY TWO EQUAL (TOP & BOTTOM) FLAT TRIANGLE SURFACES, PLUS 3 INDIVIDUAL RECTANGULAR SIDE PANELS  
_______________________________ ( Sa = 2((b x h)/2) + (a x L) + (b x L) + (c x L)  square meters, or m2 )

CIRCLE and CIRCULAR PRISM (CYLINDER)

Focus on the CIRCLE shape.

9.- How long do you think the PERIMETER of the circle (also called CIRCUMFERENCE) in the display will be?    HINT – MEASURING THE LENGTH OF THE CURVED PERIMETER OF THE CIRCLE WITH A RULER OR EVEN A TAPE IS NOT EASY. 
____________________ ( p is about  19  meters )

 10.- What would be a good formula for a quick calculation of the perimeter of the circle?    HINT – through history, many efforts were made to find “easy” ways.  The best way found, so far, is to COMPARE the length of the perimeter, called the CIRCUMFERENCE, to the length of the width of the circle, called the DIAMETER.  The diameter is therefore the length of a line across the circle, passing through its center.  The length of the diameter is abbreviated by the letter “D”.  The length of the perimeter is always a little more than 3 times (approximately 3.1416) the length of the diameter.

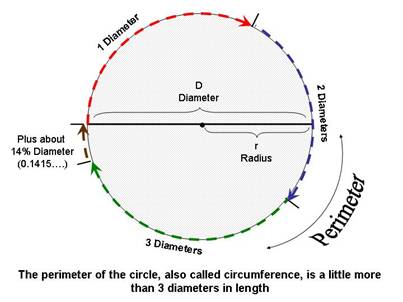
Half of the diameter, or the distance from any point on the circle to the center, is called the RADIUS, and this distance is abbreviated by the letter “r”.

The number of times the DIAMETER fits onto the CIRCUMFERENCE of a circle is approximately 3.1416.  This number is nicknamed π, or “pi”. Call the measuring and calculating the PERIMETER AND AREA OF A CIRCLE to observe the relationships of radius and diameter to the perimeter and area of a circle.

10.- What would be then a good formula for the perimeter / circumference of a circle?                        _________________________   (  C  =  π D )                         

11.- If the diameter of a circle is 6 meters, what would be the length of its circumference:   C = ? ____________ ( 3.1416 x 6.0 = 18.8496 meters )

Now focus on the flat surface inside the circle.

12.- What would be the area  of the circle, that is, the total number of unit rectangles (or “tiles”)?     HINT – COUNTING THE UNIT SQUARES AND PARTS OF UNIT SQUARES INSIDE A CIRCLE IS NOT EASY, AND THROUGH HISTORY, MANY EFFORTS WERE MADE TO FIND “EASY” WAYS TO DETERMINE THE AREA INSIDE A CIRCLE.  THE BEST WE COULD DO, UP TO TODAY, IS TO COMPARE THE AREA OF THE CIRCLE, TO THE AREA OF THE FOUR SMALL “CORNER SQUARES” THAT MAKE UP THE SQUARE THAT COVERS THE WHOLE CIRCLE. 

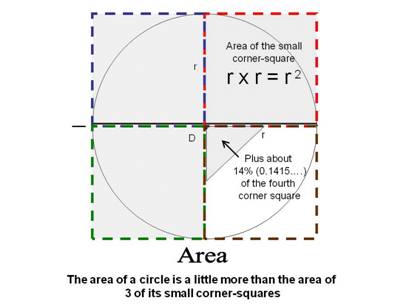
13.- Therefore, what could be a good formula to calculate the area of the circle?  
______________________ ( a =  π  x  r2 ,  square meters, or m2 )

14.- If he diameter of a circle is 3 meters, what would be its area?

     ______________________   ( π x 3.0 x 3.0  =  3.1416 x 9.0  =  28.2744 square meters, or m2 )

Now focus on the SOLID 3-dimensional CYLINDER (CIRCULAR PRISM) shape.

15.- What would be the volume of the cylinder?
AGAIN, NOT EASY TO DETERMINE BY COUNTING UNIT CUBES.

________  ( approximately  282  cubic meters, or m3 ) 

CREATIVE MEASUREMENT – VOLUME

COULD YOU THINK OF ANY OTHER GOOD, CREATIVE IDEAS ABOUT HOW TO MEASURE VOLUME WHEN WE HAVE IRREGULAR, ODD-SHAPED OBJECTS?

***   HIGHLIGHTING THE USEFULNESS OF INDIRECT MEASUREMENT

In the following case we illustrate indirect measurement of volume using the fact that the volume of an object being inmersed in a liquid is the same as the volume of the liquid being displaced.(NOTE: This is actually a common procedure used in industry, and useful when determining qualities related to intricate shaped natural or designed objects, as is the case with expensive jewelry).

An interesting consequence of this regarding the relative weights of objects being immersed in fluids (liquids or gases) is described by the Archimedes principle. This principle states that the force exerted against an immersing object is equal to the weight of the fluid being displaced. Therefore, when the weight of an object is less (less dense substance) that the weight of the fluid being displaced, it will float. Otherwise, it will sink.

16.- Another example of indirect measurement: In astronomy, remote stars, planets and other celestial objects are said to be a given number of light-years away. Can you find out what does "a light year" mean, and how they are measured?

17.- Radar speed detectors such as those used for traffic control use a beam of "radar" energy that bounces and is detected back by an instrument to determine the location, distance and speed of moving objects. Can you find out how "radar object and speed detectors" work, and their importance for warfare?

18.- What could be a formula for a quick calculation of the volume of the cylinder?    HINT – THE VOLUME OF ANY PRISM CAN BE FOUND BY COUNTING ALL THE UNIT VOLUME PIECES AND PARTS INDIVIDUALLY, or, in a more efficient way, BY FIGURING UP THE AREA OF ONE CIRCULAR FACE, THE VOLUME OF ONE SLICE, AND THEN ADDING UP ALL THE equal slices THAT MAKE UP THE LENGTH OF THE CYLINDER (PRISM).

 _____________________ ( v = a L =  (π  x  r2 ) x L  cubic meters, or m3 )

CREATIVE MEASUREMENT – INTEGRATED SURFACES

COULD YOU THINK OF ANY OTHER GOOD, CREATIVE IDEAS ABOUT HOW TO MEASURE SURFACE AREA WHEN WE HAVE ELABORATE, MULTI-SHAPED OBJECTS?

***   TIME TO HIGHLIGHT THE USEFULNESS OF INTEGRATION MEASUREMENT

19.- What would the formula for a quick calculation of the SURFACE AREA of the cylinder?    HINT – THE SURFACE AREA IS MADE UP BY TWO EQUAL (TOP & BOTTOM) CIRCLE SURFACES, PLUS ONE SIMPLE RECTANGLE AREA, WRAPPED AROUND THE TOP AND BOTTOM CIRCLES, as shown below.  

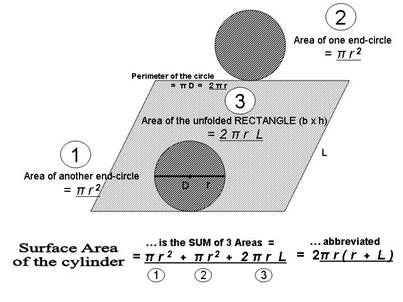
______________ ( Sa = 2( π  x  r2 )  +  ( 2 π r ) x L)  square meters, or m2 )