Counting and numbers, as a way to insure that we are dealing with the right amount of things, at the right times, seem to have been with us forever Through time, we have also learned that using grouping and appropriate symbols can help manipulate quantities more effectively. Having ten fingers in our hands, readily available to communicate and help manipulate numbers seems to have also influenced our historic preference for counting items in groups of ten. This resulted in the current decimal, or Base 10 counting system. Today, however, the overwhelming majority of calculations are not performed in Base 10, but instead in groups of two, by computers and devices using a binary or Base 2 system. Indeed, it is a binary world out there. Should we consequently be more proactive when educating our children, so as to include bases other than ten, particularly Base 2, from the earliest grades? This article proposes this to be not only feasible, but pedagogically desirable.
1.- INTRODUCTION
Through history, our survival has depended on our abilities to perceive, imagine, and transform the environment around us [1]. These abilities have been related to the intelligent use of images, symbols and numbers, to make things more efficient, safer, cheaper, faster, better. The better the representations and manipulations we have of the objects and actions in our environment, the better we can understand, and manage them.
We use representations to help us understand, imagine and transform the environment by counting and measuring the size, form and qualities of objects, groups, and actions. We do this by refering to "counts of" comparable, identifiable discrete, consecutive “basic unit” pieces that would compose the given object, group, or action, and count them as part of a whole [3]. Through careful perception, and manipulation these representations, counting and measurement can be made as accurate (free of error) and precise (reliably repeatable results) as possible, so we can make the things we do better. Through convenient images, symbols, arrangements and manipulations, we can record, communicate and process information in more effective (purposeful) and more eficient (cheaper, faster, and safer) ways [5].
Through history, different civilizations have designed a variety of number systems for counting, using particular symbols and procedures that reflected their needs and abilities. In particular, most successful number systems in our history seemed to take some advantage of our having ten fingers (digits) in our hands, obvioulsy for their computational and communication benefits. Ancient Egyptians (about 2,500 BC) used strokes and icons of special objects to represent counts (http:/www.eyelid.co.uk/numbers.htm) mostly in groups of ten. During the old Babylonian empire (about 1,800 BC), scribes carved scratches on clay tablets to record numbers representing terms of formal commercial transactions. The babylonian culture seemed to have focused particularly in groupings of 10, 12 and 60 (http://gwydir.demon.co.uk/jo/numbers/babylon/index.htm). Research in history indicates that our current scales for measuring angle degrees (30, 90, 180, 360 degrees) and time (12, 24 hours, 30 days) were influenced by the Babylonian counting systems.
The Chinese (about 500 BC) used a variety of formal and informal sets of characters to represent numbers for different occasions, mostly using groupings of 10 (http://www.mandarintools.com/numbers.html). Indeed common abacus design seems to reflect much of the structure of counting and number operations in ancient China.
The Greek (http://gwydir.demon.co.uk/jo/numbers/greek/index.htm) and the Romans (http://gwydir.demon.co.uk/jo/numbers/roman/index.htm) used elaborate combinations of symbols and letters to describe their numbers, while the Mayans (about 1,000 AD) used dots and lines, mostly to relate to moon cycles, seasons, and passage of time in general. The Mayan counting system emphasised using the numbers 5 and 20 as a basis for counting the number of days in their month. The Mayan system also preceeded most other systems in recognizing and explicitly including the number zero (conch) to signal the absence of quantity (http://gwydir.demon.co.uk/jo/numbers/maya/index.htm). The Roman numeric system relied on letter symbols or groups to represent numbers around 5 (V=5) and multiples of 10, such as X=10, L= 50, C=100, D=500, M=1000. The non-trivial, subtractive placing of adjacent symbols in groups of the Roman number system presented obvious shortcomings, particularly as compared with the contemporary, simpler, Hindi-Arabic or "decimal system", described next.
Eventually, and seemingly due to advantages of having ten fingers (digits) in our hands, as well as the simplicity of uniform groupings (i.e bundling) of units and symbols, number systems converged into the current simplified decimal system. In this system, called the Arabic, Hindi-Arabic, or Base 10 system, there are only ten basic counting symbols (1, 2, 3, 4, 5, 6, 7, 8, 9, and zero), which are used repeatedly in a series of ordered positions to signify the number of units or "bundles" of increasingly higher value, each position to the left ten times greater than the previous (1, 10, 100, 1000, 10000, etc.). Such positions are known as place values, and in the common Base 10 arrangement, the quantities indicated by the stated digit in each position has a value of bundles ten times greater than the ones next to the right (i.e. ….., x1000, x100, x10).
Egyptian
Babylonian
Chinese
Greek
Roman
Mayan
Hindi-Arabic
More recently however, accelerated developments in science and technology, particularly in electromagnetics, electronics and materials has led a shift to a number system based in only two symbols, typically represented by a zero, and a one (0, 1). Conveniently, these two symbols correspond to each of two distinct, reliably implemented and manipulated states of electronic and magnetic materials and devices. The system is called binary, or Base 2 number system, and it is conceptually the most efficient way of using a distinctive characteristic to represent information [7]. For numbers beyond 1, the binary system uses combinations of its two basic symbols, arranged in sequential space-ordered positions, representing multiples of its Base 2. Similar to the decimal system, the positions represent "bundles" that increase in value from the right to the left by multiples of 2 (i.e. …, 32, 16, 8, 4, 2, 1).
NOTE: A "base" is therefore the maximum number of items that can be counted up in each digit position, as they are bundled and transfered to be counted as a unit-bundle part of the next, higher positional value digit.
Because of the massive gains in efficiency and speed in producing, communicating and manipulating number information, binary representations are used today for practically all automated operations, with translation into the decimal system done only when human communication and participation is absolutely necessary.
Still, and in spite of its importance and relative simplicity, the topic of the binary system seems mostly absent from K-12 curricula. Why is this?
2. TEACHING DIFFERENT NUMBER BASES
Up to now, and almost exclusively, teaching to count and manipulate quantities in K-12 classrooms has been focused on the Base 10 system. How appropriate is this for today's and tomorrow's needs?
Understandably, a focus on the Base 10 system has been critical in educating citizens to operate competently in a decimal world, even today. But with technology moving into automated measurement, communications, calculation and conrol everywhere, the abilities to design, produce, and apply corresponding tools can very well define the future industrial and commercial success and dominance of organizations and nations.
Because key quantitative abilities begin to be developed (or not) into our minds and bodies during the earlier years in our lives [8], perhaps it is a good time to rethink this issue in the context of our basic elementary education and earlier, so the foundations for basic modern number and computation concepts are laid when it is more effective.
What would it take to add the topic of bases other than 10 in the K-12 curriculum?
First, to promote general numeracy, proven successful approaches, such as starting with smaller numbers and repeated counting practice should always be considered. Then, proper use of currently available technologies should be seen as opportunities to leverage student motivation for learning in context [9, 10], skill development [11], and community building [12]. Learning with technology will almost always offer helpful alternatives to increase student involvement and understanding through media [13], visual sharing, group chanting, participation and interaction. More issues related to the use of current technologies for learning and teaching can be found at: Teaching and Learning with Technology in Elementary and Secondary Classrooms (FRazo, 2010)
Following ahead are examples of teaching activities for the concepts of place value, number bases, and the Base 2 number system. Although these activities were designed and field tested with careful consideration to the technical, pedagogical, and content knowledge issues [17] of classrooms in mind, up to now there have been no large-scale tests of the activities in order to demonstrate statistical significance of their effects. Still, the evidence gathered so far through repeated experiences [14, 15, 16] point to consistent increases in student appreciation of the process of counting under different base systems, as well as of their understanding of the invariant concepts for number operations under different base systems.
3. REPRESENTATION
As an example of different representations of a number in alternative groupings or bases, the number 13 is shown in corresponding place-value representations in Bases 10, 5, and 2 in Fig 1 below. The same 13 items are shown grouped in corresponding bundles of multiples of ten, five, and two.

"13" in base 10 = "23" in base 5 = "1101" in base 2
Fig 1 Different Bases – Grouping 13 Items by 10’s, 5’s, and 2’s
Figure 2 below show images of 13 items counted in virtual counting objects (cubes or pebbles), as they were grouped in increasingly larger size bundles, as counting progresses. The links below each image provide direct access to corresponding interactive webpages on the Internet. Students can use standard Internet-enabled computers, interactive touch-screen panels and "smart boards" to access and interact with the virtual objects and scenarios performing the counting, observe, modify and learn the different counting patterns repeatedly, inexhaustibly, efficiently and safely. An image of an actual physical binary counting panel, which was designed and built by a 10th grader using a common electronic binary counter microchip and standard components, presents also an interesting option for students to experience and understand the counting process through physical enactment, imagery and real-button activation.
 |
 |
 |
|---|---|---|
The number 13 In Base 10: 13 = 10+3 |
The number 13 In Base 5: 13 = (2*5) + 3 |
The number 13 In Base 2: 13 = 8 + 4 + 1 |
Fig 2. Representing the number 13 with counters in groupings of 10, 5 and 2
4. FRACTIONS
The topic of fractions, typically introduced in the middle elementary grades, could extend to the representation of fractions in different bases. In Figure 3, the decimal number 23.675 is used to show the extension of the place value concept into fractional amounts (right of the units point), both in Bases 10 and 2, and highlighting the limitation in accuracy in representation of fractions in number systems, due to the fixed size of fractional digit units. The 2 decimal places in the decimal counter can represent only one-hundredth (0.01) block increments, whereas in the binary counter with 3 places we can represent only one-eight block increments (0.125). The binary representation that uses only 3 fractional digits is known as binary point eight, and has been used extensively in the measurement of remote (telemetry) high voltage electrical power equipment.
 |
|
Fractions in Base 10 www.animath.net/cnt10wfracx.html |
Fractions in Base 2
www.animath.net/cnt2wfracx.html |
Fig 3 Representation of the number 23.675 with fractional parts in Base 10 and in Base 2
To reduce the effect of lower accuracy of fractions due to the number of available digits in number systems and computing devices, more elaborate forms have been developed, such as doubling the number of digits used ("double word"), and using exponential factor ("floating point") representations. This topic seems important, but more appropriate for special focus at the upper grades.
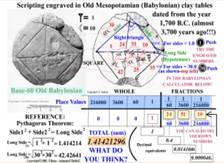
The use of place value concepts to represent fractional quantities also seems to be much older and significant than commonly assumed by both children and adults: In the interactive webpage of Figure 4 below, an ancient Babylonian clay tablet, made some 4,000 years ago, is shown including symbols and calculations describing the relationship between the sizes of sides in right triangles, and thus including fractional parts. The numbers, as stated in a Base 60 number system, correspond to a calculation commonly assumed to have been first stated in the "Pythagorean Theorem", some 2,000 years later. The buttons to the right allow the students to see in effect how the Babylonians represented the square root of 2, and the square root of the number 1,800 using their Base 60 system.
|
Old Babylonian Base 60 www.animath.net/BabylonianTablet.htm |
Fig 4 Fractions from our ancestors, some 3,700 years ago
The activity shown in Figure 5 below, titled "Inter Bases Converter" lets students enter a number in Base 10, and display its expanded (approximate) equivalent representations with fractional parts of up to 5 digits in two other arbitrary bases.
|
Inter-bases Converter www.animath.net/abasescalc.html |
Fig 5 Equivalent Representation with fractional parts in Different Number Bases
Fraction representations are also quite useful in the binary, base-2 system. The activity in Figure 6 presents an interactive process called binary successive approximation method, which is widely implemented in circuitry used to measure electrical quantities from the environment. Measurement quantities represented in binary forms are often referred to simply as digital measurements. Digital measurements of characteristics of the environment (size, weight, temperature, pressure, etc.) are created by first producing or changing voltages produced by physical sensors and transducers (converters to electrical voltage) and then evaluating these through special devices (digital meters). Digital meters typically make successively closer comparisons to known stable (calibrated) fraction segments of multiples of ½ : ½, ¼, 1/8, 1/16, 1/32, etc. within the instrument's reference voltage range. Digital meters either can run an accumulation of the smallest unit fractions (ramping), or comparing with reference fraction voltages of the instrument range to approximate (successive approximation) the unknown voltage by comparison, until matching or exceeding it. The successive approximation method, illustrated in the interactive activity of Figure 6 below, begins from the left by comparing the scaled unknown-quantity to ½ of the range, adding it to a reference-total only if the unknown is still larger. Then a comparison to a reference-total including a ¼ segment is made, which is similarly added only if the unknown-quantity is smaller than the reference-total, and so on.
In the interactive activity below, the electrical voltage of a source is controlled through a slide-knob (left), and then a successive approximation process is allowed by selecting successively smaller segments of voltage that are ½ of the previous ones each time. The process stops when the digit fraction addition causes the comparison to detect a match condition.
|
Binary successive approximation method |
Fig 6 Binary successive approximation method for electrical measurement
5. ADDITION, SUBTRACTION, AND MULTIPLICATION
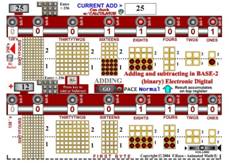
In Figure 7, the process of addition and subtraction of two numbers in Base 2 is shown, step by step, using visual virtual symbols and objects. The activity provide multi-epresentation and sensory demonstrations of digit-by-digit, place value by place value joining and regrouping of objects into larger bundles (carrying), similarly as it is done in the Base 10 system. Addition or subtraction (of the second number), is performed using the highly effective "twos complement" method. The complement of the number is its negative and therefore has the effect of subtracting, when added. The conversion can be observed by using the “+/-“ button in the display, in preparation for the subtraction operation.
|
|
Adding numbers using Base 2 binary symbols http://www.animath.net/add-2RL.htm for practice: http://www.animath.net/add-2RL-Ex1.htm , http://www.animath.net/binadd-wsheet.htm |
Add and subtract w/tokens in Base 2 http://www.animath.net/neg2.html |
Fig 7 Symbolic and physical addition and subtraction in Base 2
The process of creating a “complement of a number” replaces each digit number by its complement, or the number needed to achieve the maximum base digit value, which in the base 10 system is 9. Tthe complement of a digit valued 0 is 9, for 1 is 8, for 2 is 7, and so on. For Base 2, the complement of 0 is 1, and of 1 is 0. Consequently, the conversion of the second number into its negative equivalent (subtrahend) is achieved by the simple reversal (flipping) of each binary digit (bit) to its opposite, before adding it. The implications of this simplicity, together with the ease of implementation of corresponding binary operations are major: there is no need to provide separate additional "subtraction circuits" in electronic digital computing.
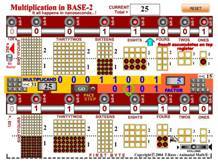
Figure 8 below presents a Base 2 replication of the standard right-to-left symbolic process, traditionally used to teach Base 10 multiplication to elementary grade children.
The activity replicates the same process using symbols and virtual pebbles and with the concept of register (temporary holding number) and shifting, being possibly emphasized to follow the right-to-left steps of the process. Due to the larger number of digits needed in binary representations, the pebble activity shown uses only eight digits (bits), or a byte, to multiply two small numbers (less than 15, and 31), accumulating the products at the top.
|
|
Multiplication w/symbols Base 2 http://www.animath.net/mult2-blocks.html |
Multiplication w/tokens in Base 2 http://www.animath.net/mult2.html |
Fig 8 Multiplication with pebbles in Base 2
6. THE PAST, THE PRESENT, AND THE FUTURE
Through time, tools have been developed to make things easier, faster, cheaper, and safer. This has also been the case for the important life-needs of counting, measuring, and more and more, for controlling and transforming the environment. Evolving from sticks and stones and life in the caves, today we find everywhere massive amounts of information and tools that can make the lives of each one of us as rich as that of royalty in previous times. In figure 9 below, four older, widely used mechanical devices, including our fingers are shown, which represented and calculated numbers in base-10 .
 |
 |
 |
|
|---|---|---|---|
| Counting w/Hands and fingers - pre-historic | Abacus - Ancient calculating device -600's BC |
Pascaline - Original base-10 calculating machine -1640's |
Commercial base-10 rotating metal-pinnion adding machine - 20th Century |
Fig 9 Primitive mechanical devices representing numbers and automating calculations in base-10
More recently, the dramatic transition from mechanical, Base 10 number representation and computation, to a Base 2 electronic and electromagnetic world has propelled, and continues to revolutionize society. Figure 10 includes images of a Base 10 /decimal mechanical accounting machine (left), which was popular in administrative offices around the middle of the twentieth century (NCR Model 32, circa 1950), the panel of an early vintage electronic Base 2 /binary digital computer (center, DEC PDP-8, circa 1965), representing the face of the sweeping electronic technologies that came to replace mechanical computing, with devices such as large scale integrated (LSI) binary circuit microchips, billions of times more powerful, and thousands of times smaller than their predecessors, in effect revolutionizing all facets of our industry, commerce, leisure and education.
 |
 |
 |
|---|---|---|
NCR Model 31 Decimal Accounting Machine -1950's |
DEC PDP-8 Binary Electronic Computer -1960's |
Current-day Binary Microchips |
Fig 10 Images of mechanical and electronic tools used to automate basic arithmetic operations
The NCR Model 32 carried accumulated additions for numbers in some 20 totals in its mechanical gears, performing parallell additions in about one second. Today's microchips can hold billions of numbers, and additions within billionths of a second, and their capabilities are still increasing. We definitely have come a long way, and in the future we will most likely be in situations, places and with needs that we can hardly imagine, but there is no question that we need to be ready and prepared for it as much as we can be. Even today, increasingly more and more different types of devices, some extremely small, affordable and efficient are already being used to assist all kinds of industrial, commercial, leisure, and common household operations. All these use almost exclusively the binary system for representation and operation of information in their applications, the result is that almost 100 percent of the computational activity is being performed automatically by electronic means and it is in the binary, Base-2 numeric system. Unfortunately, even in the latest K-12 mathematics curriculum ("Common Core", 2012 in California ), currently in the process of implementation, the Binary, Base-2 number system is not even mentioned, .
7. BASES OTHER THAN TEN IN THE K-12 CLASSROOM
During previous years, various activities, such as those presented in this document have been tried and tested, though informally, to investigate their potential to teach elementary children understand and appreciate number systems other than Base 10 [16]. The results have been positive. Not surprisingly, success in the use of virtual interactive multimedia activities seem to also be the result of proper attention to pedagogically proven approaches to teaching traditional standard Base 10 concepts and skills.
Our experience is that introducing the Base 2, usually together and in paralell understandings with those traditionally focused Base 10 concepts usually increases interest, eagerness to learn the basic concepts of place value and operations, even among lower elementary grade children. The fact that binary-Base-2 is the numeric system that is used in today's digital computers usually adds a touch of reality and excitement to the process.
8. CONCLUSIONS
As it is clear that the concepts of counting, measurement, place value, number operations and numeracy in general will continue to hold great importance in the processes of teaching and learning quantitative skills, it would seem critical that we will need to reinforce our education on these topics, to make them more relevant and motivating.
As technologies evolve, it has also become apparent that practically all number operations in the real world are becoming automated, and as a result of technological developments, numbers today and in the future are becoming lesss processed in the traditional decimal, Base 10 system, but in the binary, Base 2, binary system, and in electronic or electromagnetic data coding, computing, storage, and telecommunication devices.
In preparing our children for a life of design, production and implementation of competitive automation solutions, will seem therefore helpful to increase our attention to other usewful, non-decimal number systems, particularly the binary system.
Since the basic concepts involved in the binary system are similar, even simpler than those in the decimal system, it would also seem appropriate to consider reviewing the curricula, so the binary system can complement, support and strengthen our teachings on basic numeracy, from the earlier grades.
As the power of digital technologies grow and become more accessible, interactive multimedia is becoming more available as teaching tools, therefore there seems to be no reason why these tools could not be used to support and enrich teaching, successful traditional and new pedagogical practices. This will assist in preparing the children more effectively to be successful in the binary world they will be living in, or whichever becomes most useful in the future.
BIBLIOGRAPHY
[1] Croll, E. Parkin, D., Bush Base Forrest Farm: Culture, Environment, and Development, Rutledge, New York, 1992.
[2] Smith, D. Jekuthiel, D. & Ginsburg, D. Numbers and Numerals. W. D. Reeves, 1937.
[3] Schifter; D., A Constructivist Perspective on Teaching and Learning Mathematics, Phi Delta Kappan, Vol. 77, 1996.
[4] Stevens, S., On the Theory of Scales of Measurement, Science Vol. 103, No. 2684, 1946
[5] Dantzig, T. Number: The Language of Science. Macmillan Company, 1954.
[6] Ortenzi, E. Numbers in Ancient Times. J. Weston Walsh, 1964.
[7] Shannon, C.E., A Mathematical Theory of Communication. Bell System Technical Journal, July, 1948.
[8] Elkind, D., Formal education and early childhood education: An essential difference, Phi Delta Kappan Journal. Phi Delta Kappa International, 1986.
[9] Lave J., Cognition and practice. Cambridge University Press. Cambridge, Ma. 1993.
[10] Greeno J., Situations, mental models, and generative knowledge. In Klahr & Kotovsky, Complex Information Processing, Hillsdale, NJ. 1989.
[11] Reitman, W. R., Cognition and thought, an information processing approach. Wiley and Sons, NY, 1965.
[12] Vygotski L., Mind in Society: The Development of higher psychological processes. M Cole, et. Al (Eds), Cambridge, Ma, Harvard University Press, 1978.
[13] CISCO & The Metiri Group, Multimodal Learning Through Media: What the research says. Global Lead, Education. CISCO Systems, Inc. 2008.
[14] Razo, F., Teaching fractions in remedial mathematics using virtual manipulatives. Conference of the International Journal of Arts and Sciences Proceedings, Volume 1 (11), Las Vegas, Ne, 2008.
[15] Razo, F., Preparing teachers for the realities of technology in elementary classrooms. California Council on Teacher Education - Conference, San Diego, Ca, 2009.
[16] Razo, F., Using the Brigance II test to assess the effect of virtual manipulatives in teaching basic numeracy. Unpublished research report, Hayward, Ca, 2009.
[17] TPACK, http://www.tpack.org/ Open Internet information site, 2009.